README

Given a stream of bits and a window size N, we want be able to answer the question

How many 1s appeared in the last k bits?

Of course the answer is very simple if we are able to store in memory all last N bits. If it's not the case, we have to use a smarter way to store and to query the data.

The DGIM algorithm allows us to answer the question with a logarithmic amount of memory, and with tunable precision.

More precisely, for a given precision 1/m, the needed amount of memory is O(m log(N)²).

Just to outline, log(N)² (base 2) is a ridicously low number compared to N, for big N. For example, if N is 80 bilions, log(N)² is 1311.

In this library you can find a PHP implementation of the algorithm, together with the generalization to streams of non negative integers. Yeah, PHP is not the proper tool for memory-intensive tasks, I've written this mainly for experimental purposes.

How does it work?

The main idea is to store "buckets" of bits, with an exponential increasing size. For each bucket we store only the timestamp of its latest one and the number of ones it contains.

For more details you can check section 4.6.2 of the book Mining of Massive Datasets, freely available in PDF format.

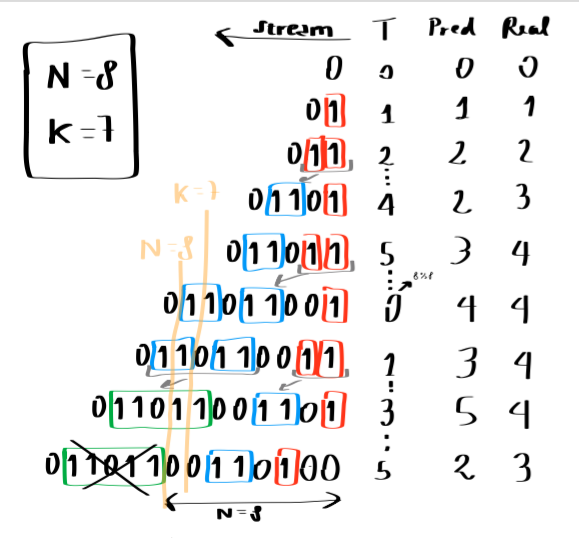
Here you can find a sketch that explains the behaviour of the algorithm for a window of 8 bits when asking the number of ones of the last 7 bits. As you can see, when there are more than two buckets of the same size, the two oldest are condensed into a twice sized one. Timestamps are stored modulo N.

To calculate the sum of last K bits, we find the earliest bucket whose timestamp is in the k-window, we take an half of its value, and we sum to it the sizes of all the following buckets.

Counting 1s

The only component the client need to use is the Counter class. This is the way to use it for counting ones with a max 1% error:

use NicMart\DGIM\Counter;

$precision = 0.01;
$m = (int) (1/$precision) + 1;

$counter = new Counter($windowSize, 1, $m);

for ($i = 0; $i < 100000; $i++) {
    $counter->input(rand(0,1));
}

$onesInLast1000 = $counter->getCount(1000);
$onesInLast10000 = $counter->getCount(10000);

Counting the sum of positive integers

If you are dealing with a stream of positive integers instead of a stream of bits, you can use the counter to get the approximate sum of the last $k ints. To do that you need to pass to the Counter the maximum of the integers you will receive in the stream:

The only component the client need to use is the Counter class. This is the way to use it for counting ones with a max 1% error:

$counter = new Counter($windowSize, $maxIntOfTheStream, $m);

for ($i = 0; $i < 100000; $i++) {
    $counter->input(rand(0,$maxIntOfTheStream));
}

$sumOfLast1000 = $counter->getCount(1000);
$sumOfLast10000 = $counter->getCount(10000);

Command line example

You can test the precision of the library on randomly generated data using the examples/example.php file:

php example.php           
Test example to check the precision of the algorithm compared to real data.
Usage: php example.php windowsize maxint precision.
Example: php example.php 1000 100 0.1

php example.php 3000 10 0.01
...
N: 1066
Predicted: 5405
Real: 5405
Error: 0%
--------------------
N: 1599
Predicted: 8023
Real: 8034
Error: 0.14%
--------------------
N: 2398
Predicted: 12079
Real: 12108
Error: 0.24%
--------------------
Average Error: 0.042
Max Error: 0.24

References

You can find a detailed description of the algorithm in section 4.6.2 of the wonderful book Mining of Massive Datasets, freely available in PDF format.

Technical notes

Each bucket stores the timestamp and the exponent as php integers. The most memory efficient implementation should only stores log(N) bits for the timestamp and log(log(N)) bits for the exponent.

Furthermore, the bucket sequence is implemented as a double linked list, so it is taking space also for the bucket links. An array implementation of the sequence and a language that provides true array objects can avoid this.

Install

The best way to install DGIM is through composer.

Just create a composer.json file for your project:

{
    "require": {
        "nicmart/dgim": "~0.1"
    }
}

Then you can run these two commands to install it:

$ curl -s http://getcomposer.org/installer | php
$ php composer.phar install

or simply run composer install if you have have already installed the composer globally.

Then you can include the autoloader, and you will have access to the library classes:

<?php
require 'vendor/autoload.php';

nicmart / dgim

Maintainers

Details