mgrechanik/ant-colony-optimization

The implementation of the Ant colony optimization algorithm

1.0.0 2023-12-06 05:40 UTC

Requires

• php: ^8.0

Requires (Dev)

• phpunit/phpunit: 10
• yoast/phpunit-polyfills: ^2.0

BSD-3-Clause

• Mikhail Grechanik

• php
• graph
• tsp
• Ant colony optimization
• Travelling salesman problem
• Shortest path problem
• aco
• Asymmetric travelling salesman problem
• Symmetric travelling salesman problem
• Constrained Shortest Path First
• Optimization method
• Optimization algorithm
• Search algorithm
• Artificial ants
• model-based search
• shortest paths
• path planning

README

Русская версия

Table of contents

• Introdution
• Demo
• Installing
• How to use
• Settings
• Performance
• TSPLIB95
• Terminology

Introdution

The Ant colony optimization is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs (from Wikipedia).

The task we are solving could be either "Travelling salesman problem" or "Shortest path problem", or Constrained Shortest Path First, etc.
The two first tasks are solved within this library.

There are a lot of strategies and variations of Classic ACO algorithm.
This library out of the box implements Classic ACO and ACO with elitist ants.

The library could be easily extended so you can implement your ACO variations and to solve the tasks you need.

The initial data about the graph comes either from adjacency matrix or from a list of nodes (cities, vertices, etc) with their X and Y coordinates.

The work of library had been tested with TSPLIB95 data sets, so we could check it's performance and efficiency.

Amount of ants, all coefficients and parameters could be changed to your need.

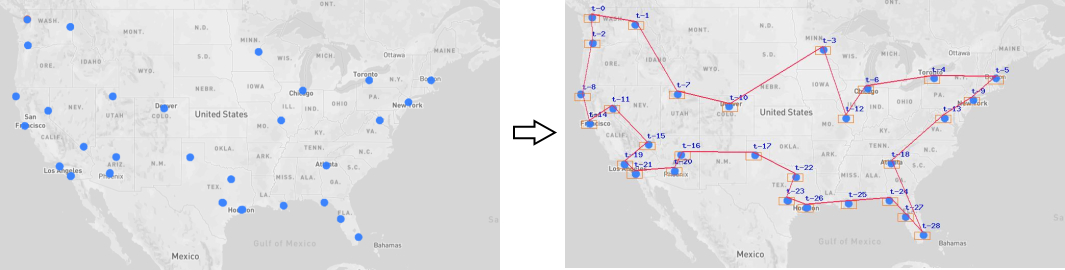
Now we have a web app which you can install and run locally to practice with this algorithm. Look for it's video demo for details.

Demo

Solving the travelling salesman problem with the ant colony optimization algorithm:

Another example:

Installing

Installing through composer::

The preferred way to install this library is through composer.

Either run

composer require --prefer-dist mgrechanik/ant-colony-optimization

or add

"mgrechanik/ant-colony-optimization" : "~1.0.0"

to the require section of your composer.json.

How to use

Basic API

1. Creating a Manager with the dependencies we need

Manager::__construct(DistanceInterface $distanceStrategy = null, AFinder $finder = null, 
                     MathematicsInterface $mathematics = null, Task $task = null);

      - By default Finder will be Classic one, and the Task will be the Travelling salesman problem

1. Loading data from an adjacency matrix

$manager->setMatrix(array $matrix, int $nameStart = 0)

      - $nameStart - from which number start naming aliases of nodes

1. Loading data from an array of cities

$manager->setCities(City ...$cities)

      - This array of cities will be transformed to adjacency matrix. Distances will be calculated according to the strategy we set to a Manager.
      - If city has a name property it will become it's name alias

1. Changing of the adjacency matrix

$manager->updateMatrix(int $y, int $x, float|int $value, bool $double = true)

      - For example we could make some path impassable - $manager->updateMatrix(1, 0, 1000000);

1. Run the computational process

$distance = $manager->run(int $iterations = 400)

      - for small graphs we could reduce amount of iterations.
      - It will return the distance we found or null when the search gave no result

1. Getting the path we found

$path = $manager->getInnerPath()

      - The path we found who consists of node's numbers.
      All nodes are internally named as numbers from 0 to N-1, where N is node's amount.

1. Getting aliased path we found

$path = $manager->getNamedPath()

      - The path we found which consists of node's name aliases, if we set them.

Examples

Solving "Travelling salesman problem" with Classic ACO

use mgrechanik\aco\Manager;

$manager = new Manager();
$matrix = [
            [ 0, 8, 4, 11],
            [ 8, 0, 9, 5 ],
            [ 4, 9, 0, 8 ],
            [11, 5, 8, 0 ]
          ];
$manager->setMatrix($matrix);
$distance = $manager->run(20);
var_dump('Distance=' . $distance);
var_dump($manager->getInnerPath())

We will get:

Distance=25

Array
(
    [0] => 0
    [1] => 1
    [2] => 3
    [3] => 2
    [4] => 0
) 

Solving "Shortest path problem" with Classic ACO

use mgrechanik\aco\Manager;
use mgrechanik\aco\SppTask;

$task = new SppTask(0, 3);
$manager = new Manager(task : $task);
$matrix = [
            [ 0 , 8, 4, 100],
            [ 8 , 0, 9, 5  ],
            [ 4 , 9, 0, 8  ],
            [100, 5, 8, 0  ]
          ];
$manager->setMatrix($matrix);   
$finder = $manager->getFinder();
// increase amount of ants to 6
$finder->setM(6);
$distance = $manager->run(50);
var_dump('Distance=' . $distance);
var_dump($manager->getInnerPath())

We will get:

Distance=12

Array
(
    [0] => 0
    [1] => 2
    [2] => 3
)
// for comparison, the direct path [0, 3] is closed by big distance and distance of path [0, 1, 3] is 13

Loading data as an array of cities

use mgrechanik\aco\Manager;
use mgrechanik\aco\City;

$cities = [new City(10,10), new City(50,50), new City(10,50), new City(60,10)];
$manager = new Manager();
$manager->setCities(...$cities);

Loading data as an adjacency matrix

use mgrechanik\aco\Manager;

$matrix = [
            [ 0, 8, 4, 11],
            [ 8, 0, 9, 5 ],
            [ 4, 9, 0, 8 ] ,
            [11, 5, 8, 0 ]
          ];
$manager = new Manager();
$manager->setMatrix($matrix);

Using the Elitist Finder

$finder = new \mgrechanik\aco\elitist\Finder();
$manager = new Manager(finder : $finder);
//...

Have a look at the history of our work - best solutions we had been finding

use mgrechanik\aco\Manager;

$matrix = [
            [ 0, 8, 4, 11],
            [ 8, 0, 9, 5 ],
            [ 4, 9, 0, 8 ] ,
            [11, 5, 8, 0 ]
          ];
$manager = new Manager();
$finder = $manager->getFinder();
$manager->setMatrix($matrix);
$manager->run();
var_dump($finder->getHistory());

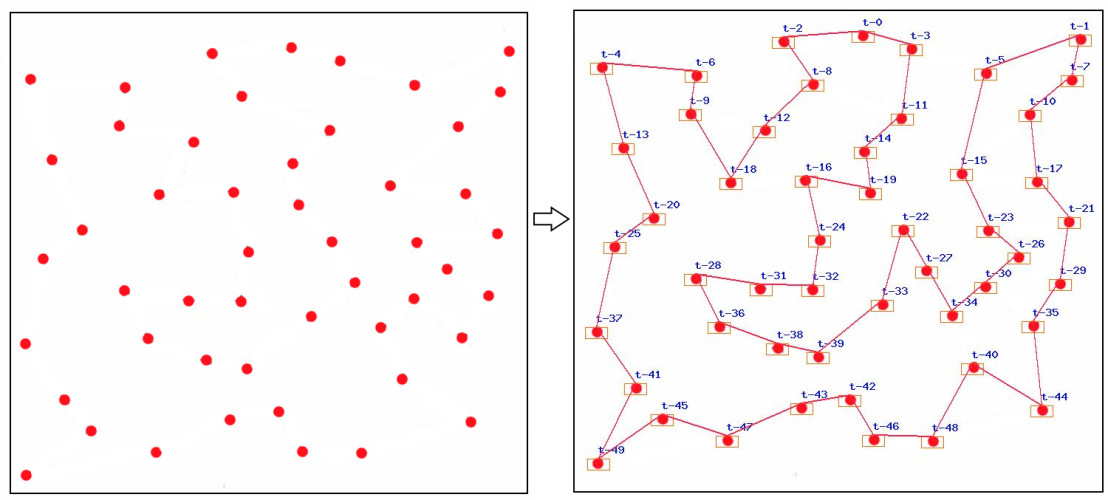
Loading a list of cities from an image file

With the use of this library we can load a list of cities from the image. And the result of the search could be displayed on the image too. It will look like images on Demo.

Read docs of that library for more information how to prepare images but briefly it is this: On white canvas draw points of 10 px diameter (they are vertices of the graph) and use this image with the code below

use mgrechanik\aco\Manager;
use mgrechanik\aco\City;

try {
    $imageSearcher = new \mgrechanik\imagepointssearcher\Searcher(
        './images/your_image.jpg',
    );
    $found = $imageSearcher->run();    
    if ($found > 1) {
        $points = $imageSearcher->getPoints();
        $cities = [];
        foreach ($points as $point) {
            $cities[] = new City($point['x'], $point['y']);
        }    
        $manager = new Manager();
        $manager->setCities(...$cities);
        if ($res = $manager->run()) {
            $innerPath = $manager->getInnerPath();
            $imageResult = new \mgrechanik\imagepointssearcher\ImageResult($imageSearcher);
            $imageResult->drawLabels();
            $imageResult->drawMargins();
            $imageResult->drawPath($innerPath);
            $imageResult->save('./images/result.jpg');
        }
    }
  
} catch (Exception $e) {
    //
}

Settings

Finder settings

The base object we tune is the Finder.
Lets get it:

$manager = new Manager();
$finder = $manager->getFinder();
// Settings
//$finder->set...
// ...
//$manager->run();

Settings available:

• Set the distance value which makes the path between two nodes impassable
  ->setClosedPathValue(int $value)

• Set amount of ants
  ->setM(int $m)

• Set amount of ants in percents relatively to amount of nodes. Default behavior (=40%)
  ->setMPercent(int $mPercent)

• Set the coefficients for formulas

->setAlpha(float $alpha);
->setBeta(float $beta);
->setP(float $p);
->setC(float $c);
->setQ(int $q);

• Set the strategy to do the mathematical work
  ->setMathematics(MathematicsInterface $mathematics)

• Set the task we are solving. Say TSP, SPP or other.
  ->setTask(Task $task)

• Set an amount of elitist ants (when we use Elitist Finder)
  ->setSigma(int $sigma)

• Set an amount of elitist ants in percents relatively to amount of regular ants. Default behavior (=50%) (when we use Elitist Finder)
  ->setSigmaPercent(int $sPercent)

Performance

First of all turn off XDebug or it's analogies, since they could significantly affect the time the algorithm works

This ACO algorithm finds good paths on a graph. And sometimes even best paths.

Lets take, for example, the berlin52.tsp task from TSPLIB95 library, which has 52 nodes.
Solving this task with the next code:

$cities = TspLibLoader::loadCitiesFromEuc2dFile(__DIR__ . '/images/data/berlin52.tsp');
$finder = new \mgrechanik\aco\elitist\Finder();
$finder->setSigmaPercent(150);
$finder->setMPercent(30);
$finder->setAlpha(0.7);
$manager = new Manager(finder : $finder);
$manager->setCities(...$cities);
$distance = $manager->run(300);
var_dump('Distance=' . $distance);
var_dump($finder->getHistory());

We will see:

Distance=7542

   Array ... 
    [85] => Array
        (
            [distance] => 7542
            [inner_path] => 0_21_30_17_2_16_20_41_6_1_29_22_19_49_28_15_45_43_33_34_35_38_39_36_37_47_23_4_14_5_3_24_11_27_26_25_46_12_13_51_10_50_32_42_9_8_7_40_18_44_31_48_0
            [iteration] => 85
            [time_spent] => 1.94 sec
        )  
    )

This code, working on an office computer, found the best path ever known for less than 2 seconds.

We used here Elitist ACO algorithm since in practice it gives better results than Classic one.

An Algorithm is probabilistic, ants travel differently each new search. A lot depends upon amount of nodes, amount of ants, all coefficients and parameters used with formulas.

TSPLIB95

The TSPLIB95 library ships with a lot of Travelling salesman problems - initial data and solutions - best results ever found for these tasks (paths and distances).

The library is valuable that with it's data we could test the efficiency of our algorithms, coefficients and parameters.

The library consists of a lot of different initial data formats. Out of the box we support two of them.

Loading data as a set of X and Y coordinates of cities. Distance is euclidean.

Example of the file with this format - berlin52.tsp .
Loading the list of nodes (cities) and transfer it to Manager:

use mgrechanik\aco\TspLibLoader;
use mgrechanik\aco\Manager;

$fileName = __DIR__ . '/berlin52.tsp';
$cities = TspLibLoader::loadCitiesFromEuc2dFile($fileName);
$manager = new Manager();
$manager->setCities(...$cities);

Loading data as an adjacency matrix

Example of the file with this format - bays29.tsp .
Loading the adjacency matrix and transfer it to Manager:

use mgrechanik\aco\TspLibLoader;
use mgrechanik\aco\Manager;

$fileName = __DIR__ . '/bays29.tsp';
$matrix = TspLibLoader::loadMatrixFromExplicitMatrixFile($fileName);
$manager = new Manager();
// tsplib95 library names nodes starting with "1"
$manager->setMatrix($matrix, 1);

Terminology

ACO - Ant colony optimization algorithm

Nodes - Nodes or vertices or cities. Ants travel between them.

Adjacency Matrix - Adjacency Matrix sets the distances between graph nodes. It is a basic structure our algorithm starts work with.

When graph is loaded like Cities with their coordinates, this information will be converted to Adjacency Matrix

Classic Finder - Finder who implements Classic ACO algorithm

Elitist Finder - Finder who implements ACO algorithm when we use elitist ants

Ant - ant, working unit, who move through the graph searching for the paths

Task - The task we are solving on the graph. For example it could be "Travelling salesman problem" or "Shortest path problem". Or other.

TSP - Travelling salesman problem. With this library we can solve both symmetric and asymmetric types of tsp

Manager - The manager which task is to form adjacency matrix , give it to Finder to solve Task.

Iteration - The iteration during which all ants find one path and put pheromones on it. We set amount of iterations themselves.

Pheromon - is the instance ants leave on paths

m - Amount of ants

mPercent - Amount of ants in percents relatively to the amount of nodes

sigma - Amount of elitist ants, if we use corresponding algorithm

sigmaPercent - Amount of elitist ants in percents relatively to the amount of regular ants

alpha - The coefficient to control the influence of pheromone amount

beta - The coefficient to control the influence of desirability of path

p - The evaporation coefficient

c - The starting amount of pheromones on paths

Q - The constant used to calculate how many pheromones an ant puts on the path it found