dbeurive/graph

This package contains the implementation of various graphs' algorithms

1.0.3 2017-01-07 11:02 UTC

Requires (Dev)

• phpunit/phpunit: >=5.5.0

Common Attribution-NonCommercial 4.0 International license

• Denis BEURIVE

• graph
• Algorithm
• dijkstra
• Tarjan
• Breadth First Search
• Depth First Search

README

• Introduction
• License
• Installation
• Graphs' types
• Graphs' representations
  • Directed graphs
    • Directed and unweighted
    • Directed and weighted
  • Undirected graphs
    • Undirected and unweighted
    • Undirected and weighted
• Graphs' API
  • Introduction
  • Loading a graph from a CSV file
    • Loading CSV with the default loader
    • Loading CSV with a customized loader
  • Dumping a graph into a CSV file
    • Dumping into CSV with the default dumper
    • Dumping into CSV with a customized dumper
  • Dumping a graph into its GraphViz representation
• Using the algorithms
  • The "Breadth First Search" algorithm
    • Synopsis
  • The "Depth First Search" algorithm
    • Synopsis
  • The Dijkstra's algorithm
    • Synopsis
    • Illustration
  • The Tarjan's algorithm
    • Synopsis
    • Illustration

Introduction

This repository contains the implementations of various algorithms for graphs.

• The breadth-first search algorithm
• The depth-first search algorithm
• The Dijkstra's algorithm
• The Tarjan's strongly connected components algorithm

License

This code is published under the following license:

Creative Common Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)

See the file LICENSE.TXT

Installation

From the command line:

composer require dbeurive/graph

Or, from within the file composer.json:

"require": {
    "dbeurive/graph": "*"
}

Graphs' types

Graphs may be:

• Directed or not.
• Weighted or not.

A given graph may be:

Type of graph	Class
Directed and unweighted	\dbeurive\Graph\lists\DirectedUnweighted
Directed and weighted	\dbeurive\Graph\lists\DirectedWeighted
Undirected and unweighted	\dbeurive\Graph\lists\UndirectedUnweighted
Undirected and weighted	\dbeurive\Graph\lists\UndirectedWeighted

Graphs' representations

Many formalisms may be used to represent a graph. For example:

• Edge lists
• Adjacency matrices
• Adjacency lists

This document presents various ways used to represent graphs:

https://fr.khanacademy.org/computing/computer-science/algorithms/graph-representation/a/representing-graphs

This PHP module uses the formalism known as "Adjacency lists".

Directed graphs

Vertices have successors (and predecessors).

We can choose to describe the graph through its lists of successors or through its lists of predecessors.

Directed and unweighted

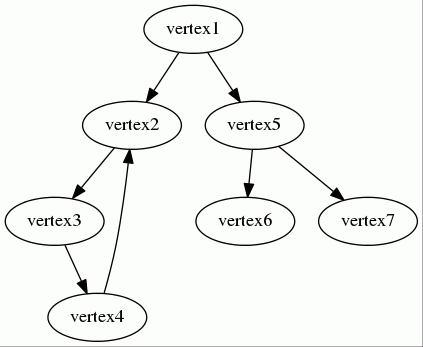
Let's consider the following directed unweighted graph:

The agency lists can be represented by the associative array below:

array(
    'vertex1' => array('vertex2' => null, 'vertex5' => null),
    'vertex5' => array('vertex6' => null, 'vertex7' => null),
    'vertex2' => array('vertex3' => null),
    'vertex3' => array('vertex4' => null),
    'vertex4' => array('vertex2' => null)
)

Or by a CSV file:

vertex1 vertex2 vertex5
vertex5 vertex6 vertex7
vertex2 vertex3
vertex3 vertex4
vertex4 vertex2

• The vertex vertex1 has two successors: vertex2 and vertex5.
• The vertex vertex2 has one successor: vertex3.
• ...

See this example.

Directed and weighted

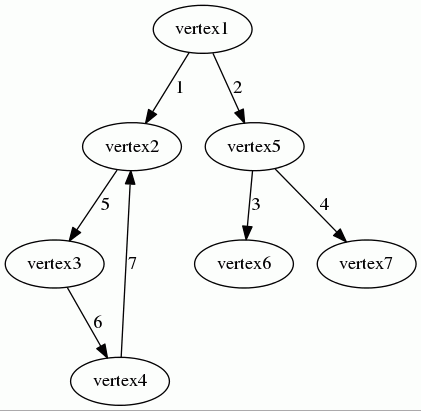
Let's consider the following directed weighted graph:

The agency lists can be represented by the associative array below:

array(
    'vertex1' => array('vertex2' => 1, 'vertex5' => 2),
    'vertex5' => array('vertex6' => 3, 'vertex7' => 4),
    'vertex2' => array('vertex3' => 5),
    'vertex3' => array('vertex4' => 6),
    'vertex4' => array('vertex2' => 7)
)

Or by a CSV file:

vertex1 vertex2:1 vertex5:2
vertex5 vertex6:3 vertex7:4
vertex2 vertex3:5
vertex3 vertex4:6
vertex4 vertex2:7

• The vertex vertex1 has two successors: vertex2 and vertex5.
  • The weight associated to the edge from vertex1 to vertex2 is 1.
  • The weight associated to the edge from vertex1 to vertex5 is 2.
• The vertex vertex2 has one successor: vertex3.
  • The weight associated to the edge from vertex2 to vertex3 is 5.
• ...

See this example.

Undirected graphs

Vertices have neighbours.

Undirected and unweighted

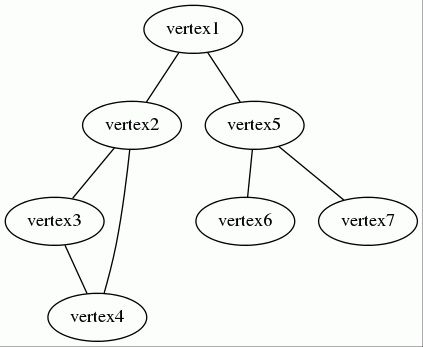
Let's consider the following undirected unweighted graph:

The agency lists can be represented by the associative array below:

array(
    'vertex1' => array('vertex2' => null, 'vertex5' => null),
    'vertex5' => array('vertex6' => null, 'vertex7' => null),
    'vertex2' => array('vertex3' => null),
    'vertex3' => array('vertex4' => null),
    'vertex4' => array('vertex2' => null)
);

Or by the CV file:

vertex1 vertex2 vertex5
vertex5 vertex6 vertex7
vertex2 vertex3
vertex3 vertex4
vertex4 vertex2

• The vertex vertex1 has two neighbours: vertex2 and vertex5.
• The vertex vertex1 has two neighbours: vertex6 and vertex7.
• ...

See this example.

Undirected and weighted

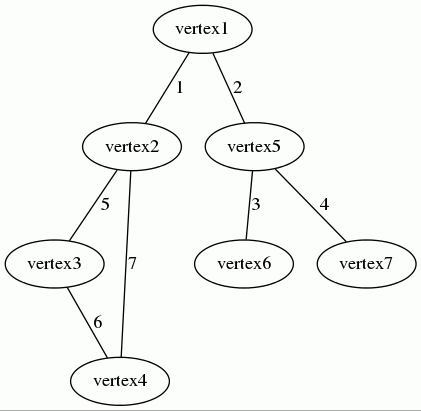
Let's consider the following undirected weighted graph:

The agency lists can be represented by the associative array below:

array(
    'vertex1' => array('vertex2' => 1, 'vertex5' => 2),
    'vertex5' => array('vertex6' => 3, 'vertex7' => 4),
    'vertex2' => array('vertex3' => 5),
    'vertex3' => array('vertex4' => 6),
    'vertex4' => array('vertex2' => 7)
);

Or by the CSV file:

vertex1 vertex2:1 vertex5:2
vertex5 vertex6:3 vertex7:4
vertex2 vertex3:5
vertex3 vertex4:6
vertex4 vertex2:7

• The vertex vertex1 has two successors: vertex2 and vertex5.
  • The weight associated to the edge from vertex1 to vertex2 is 1.
  • The weight associated to the edge from vertex1 to vertex5 is 2.
• The vertex vertex2 has one successor: vertex3.
  • The weight associated to the edge from vertex2 to vertex3 is 5.
• ...

See this example.

Graphs' API

Introduction

The graph's API allows the following actions:

• Load a graph from a CSV file.
• Dump a graph into a CSV file.
• Create the GraphViz representation of a graph.
• "Complete" a graph's representation.
• For directed graphs: calculate the lists of predecessors from the lists of successors and vice versa.

Instead of presenting an-in depth description of the API, we will show examples of uses.

Detailed API description can be generated using phpDocumentor. Just go to the root directory of this package and issue the following command: phpdoc. The documentation will be generated within the directory doc/api.

Loading a graph from a CSV file

Loading CSV with the default loader

Synopsis:

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->loadSuccessorsFromCsv($csvSuccessorsPath);
$graph->loadPredecessorsFromCsv($csvPredecessorsPath);

$graph = new UndirectedUnweighted(); // or UndirectedWeighted
$graph->loadNeighboursFromCsv($csvSuccessorsPath);

By default:

• Fields are separated by a space.
• Edges' weight is indicated by the character ':'.
• Vertices' names are loaded "as is".

Examples of standard CSV files:

vertex1
vertex2 vertex1 vertex4
vertex5 vertex1
vertex6 vertex5
vertex7 vertex5
vertex3 vertex2
vertex4 vertex3

or:

vertex1
vertex2 vertex1:1 vertex4:7
vertex5 vertex1:2
vertex6 vertex5:3
vertex7 vertex5:4
vertex3 vertex2:5
vertex4 vertex3:6

See example from-csv-directed-unweighted.php.

See example from-csv-directed-weighted.php.

See example from-csv-undirected-unweighted.php.

See example from-csv-undirected-weighted.php.

Loading CSV with a customized loader

Synopsis:

$graph = new DirectedUnweighted(); // or UndirectedUnweighted
$graph->setFieldSeparator(';');
$graph->setVertexUnserializer(function($inVertex) { return strtoupper($inVertex); });
$graph->setLinePreProcessor(function($inLine) { return trim($inLine); });

$graph = new DirectedWeighted(); // or UndirectedWeighted
$graph->setFieldSeparator(';');
$graph->setVertexUnserializer(function($inVertex) { return strtoupper($inVertex); });
$graph->setLinePreProcessor(function($inLine) { return trim($inLine); });
$graph->setWeightIndicator('::');

While loading CSV files, it is possible to specify non-standard attributes:

• The field separator. The default field separator is the space (" ").
• The weight indicator (for weighted graphs only). The default weight indicator is the character ":".

It is also possible to specify actions applied to the following data:

• The vertices' names.
• The line of CSV (for example, you can remove leading and trailing spaces).

Actions are specified via a "callable" (see this explanation).

In the following examples:

• We changed the field separator (we use ";" instead of " ").
• We changed the weight indicator (we used "::" instead of ":").
• We convert vertices' names into uppercase.
• We remove leading and trailing spaces from each line before any other process.

See example from-csv-directed-unweighted-non-standard.php.

See example from-csv-directed-weighted-non-standard.php.

Dumping a graph into a CSV file

Dumping into CSV with the default dumper

Synopsis:

$graph = new DirectedUnweighted();        // Or DirectedWeighted
$graph->setSuccessors($listOfSuccessors); // You can also set the lists of predecessors.
$graph->dumpSuccessorsToCsv($csvPath);    // You can also dump the lists of predecessors.

$graph = new UndirectedUnweighted();      // Or UndirectedWeighted
$graph->setNeighbours($listOfNeighbours);
$graph->dumpNeighboursToCsv($csvPath);

See example to-csv-directed-unweighted.php.

See example to-csv-directed-weighted.php.

See example to-csv-undirected-unweighted.php.

See example to-csv-undirected-weighted.php.

Dumping into CSV with a customized dumper

Synopsis:

// Directed Weighted

$graph = new DirectedWeighted();
$graph->setSuccessors($listOfSuccessors);
$graph->calculatePredecessorsFromSuccessors();
$graph->setFieldSeparator(';');
$graph->setVertexSerializer(function($inVertex) { return strtoupper($inVertex); });
$graph->setWeightIndicator('::');
$graph->dumpSuccessorsToCsv($csvPath);
$graph->dumpPredecessorsToCsv($csvPath);

// Directed Unweighted

$graph = new DirectedUnweighted();
$graph->setSuccessors($listOfSuccessors);
$graph->calculatePredecessorsFromSuccessors();
$graph->setFieldSeparator(';');
$graph->setVertexSerializer(function($inVertex) { return strtoupper($inVertex); });
$graph->dumpSuccessorsToCsv($csvPath);
$graph->dumpPredecessorsToCsv($csvPath);

// Undirected Weighted

$graph = new UndirectedWeighted();
$graph->setFieldSeparator(';');
$graph->setWeightIndicator('::');
$graph->setVertexSerializer(function ($inVertex) { return strtoupper($inVertex); } );
$graph->setNeighbours($listOfNeighbours);
$graph->dumpNeighboursToCsv($csvPath);

// Undirected Unweighted

$graph = new UndirectedUnweighted();
$graph->setFieldSeparator(';');
$graph->setVertexSerializer(function ($inVertex) { return strtoupper($inVertex); } );
$graph->setNeighbours($listOfNeighbours);
$graph->dumpNeighboursToCsv($csvPath);

While dumping CSV files, it is possible to specify non-standard attributes:

• The field separator. The default field separator is the space (" ").
• The weight indicator (for weighted graphs only). The default weight indicator is the character ":".

It is also possible to specify actions applied to the following data:

• The vertices' names.

Actions are specified via a "callable" (see this explanation).

See example to-csv-directed-unweighted-non-standard.php.

See example to-csv-directed-weighted-non-standard.php.

See example to-csv-undirected-unweighted-non-standard.php.

See example to-csv-undirected-weighted-non-standard.php.

Dumping a graph into its GraphViz representation

Synopsis:

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->setSuccessors($listOfSuccessors);
$txt = $graph->dumpSuccessorsToGraphviz();
$graph->calculatePredecessorsFromSuccessors();
$txt = $graph->dumpPredecessorsToGraphviz();

$graph = new UndirectedUnweighted(); // or UndirectedWeighted
$graph->setNeighbours($listOfNeighbours);
$txt = $graph->dumpNeighboursToGraphviz();

Please note that the generated GraphViz representation is highly customisable. The methods dumpSuccessorsToGraphviz, dumpPredecessorsToGraphviz and dumpNeighboursToGraphviz take parameters. These parameters allow you to customise the appearances of the vertices and of the edges.

See example to-graphviz-directed-unweighted.php.

See example to-graphviz-directed-weighted.php.

See example to-graphviz-undirected-unweighted.php.

See example to-graphviz-undirected-weighted.php.

Using the algorithms

The "Breadth First Search" algorithm

See the description here.

Synopsis

$vertices = array();

// Define a callback that will be executed for each visited vertex.
// * If the function returns true, then the exploration of the graph continues.
// * If the function returns false, then the exploration of the graph ends.

$callback = function($inVertex) use(&$vertices) {
    $vertices[] = $inVertex;
    return true;
};

// For directed graphs

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->setSuccessors($successors, true);
$graph->calculatePredecessorsFromSuccessors();
$algo = new DirectedBreadthFirstSearch($graph, $callback);
$algo->followSuccessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the sucessors.
$algo->followPredecessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the predecessors.

// For undirected graphs

$graph = new UndirectedUnweighted(); // or UndirectedWeighted
$graph->setNeighbours($successors, true);
$algorithm = new UndirectedBreadthFirstSearch($graph, $callback);
$algorithm->run('e1', $callback); // Start traversing the graph.

Please note that this algorithm works for directed and undirected graphs.

Please note that the returned value of the callback function ($callback) determines the behaviour of the method run().

• If the callback function returns the value true, then the method run() continues the traversal of the graph.
• If the callback function returns the value false, then the method run() stops the traversal of the graph.

See example breadth-first-search-directed.php.

See example breadth-first-search-undirected.php.

The "Depth First Search" algorithm

See the description here.

Synopsis

$vertices = array();

// Define a callback that will be executed for each visited vertex.
// * If the function returns true, then the exploration of the graph continues.
// * If the function returns false, then the exploration of the graph ends.

$callback = function($inVertex) use(&$vertices) {
    $vertices[] = $inVertex;
    return true;
};

// For directed graphs

$graph = new DirectedUnweighted(); // Or DirectedWeighted 
$graph->setSuccessors($successors, true);
$graph->calculatePredecessorsFromSuccessors();
$algo = new DirectedDepthFirstSearch($graph, $callback);
$algo->followSuccessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the successors.
$algo->followPredecessors();
$algo->run('e1', $callback); // Start traversing the graph from the vertex 'e1', following the predecessors.

Please note that this algorithm works for directed and undirected graphs.

Please note that the returned value of the callback function ($callback) determines the behaviour of the method run().

• If the callback function returns the value true, then the method run() continues the traversal of the graph.
• If the callback function returns the value false, then the method run() stops the traversal of the graph.

See example depth-first-search-directed.php.

See example depth-first-search-undirected.php.

The Dijkstra's algorithm

See the description here.

• This algorithm works for both directed and undirected graphs.
• The graph must be weighted.

Synopsis

// With directed graphs

$graph = new DirectedWeighted();
$graph->setSuccessors($successors, true);
$algorithm = new DirectedDijkstra($graph);
$algorithm->followSuccessors();
$distances = $algorithm->run($vertexName); // Start the algorithm.
$txt = $algorithm->dumpToGraphviz(); // For a nice representation of the result.

// With undirected graphs

$graph = new UndirectedWeighted();
$graph->setNeighbours($neighbours, true);
$algorithm = new UndirectedDijkstra($graph);
$distances = $algorithm->run($vertexName);
$txt = $algorithm->dumpToGraphviz(); // For a nice representation of the result.

See example dijkstra-directed.php.

See example dijkstra-undirected.php.

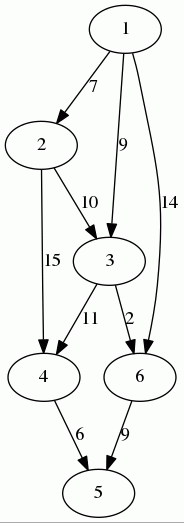
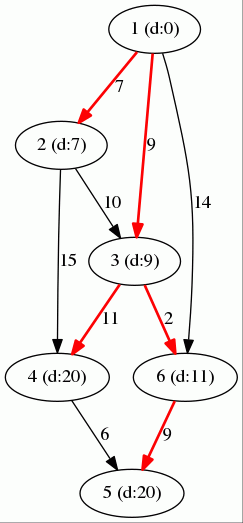
Illustration

Given the graph below, let's find the shortest paths from the vertex "1" to all other vertices.

After running the algorithm, we get:

• The shortest distance between vertex "1" and vertex "3" is 9.
• The shortest distance between vertex "1" and vertex "6" is 11.
• The shortest distance between vertex "1" and vertex "5" is 20.
• ...

Shortest paths are printed in red.

The Tarjan's algorithm

See the description here.

• This algorithm works for both directed graphs only.
• The graph may be weighted or not.

Synopsis

$graph = new DirectedUnweighted(); // or DirectedWeighted
$graph->setSuccessors($successors, true);

$algorithm = new DirectedTarjan($graph);
$algorithm->followSuccessors();
$scc = $algorithm->run();
$cycles = $algorithm->getCycles();
$txt = $algorithm->dumpToGraphviz(); // For a nice representation of the result.

See example tarjan.php.

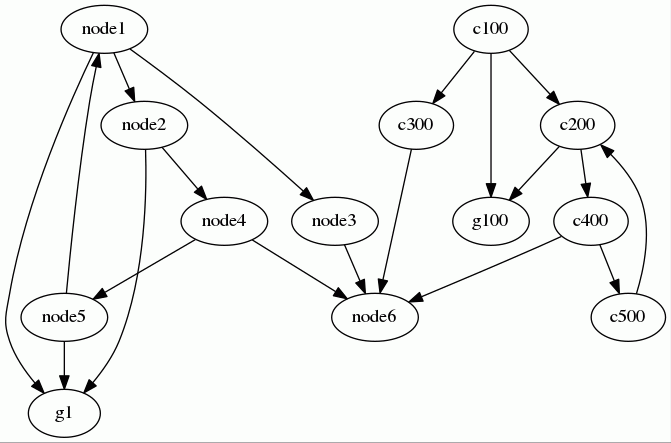
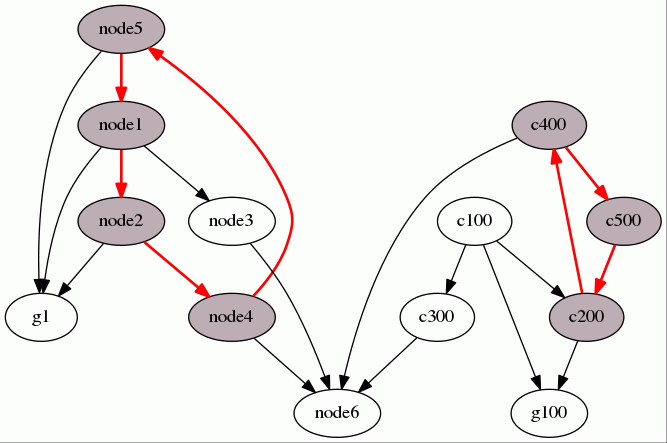
Illustration

Given the graph below, let's find all the cycles:

After running the algorithm, we get:

Please note that this algorithm does not return the list of cycles within the graph. It returns the list of strongly connected components. However, cycle detection is an application of this algorithm. Here, we choose to show the result of the method getCycles().